Calibration with a square wave (step) signal
Guralp digitisers provide calibration signal generators to help you set up your sensors. Calibration is most easily done through a PC running Guralp’s Scream! software, but you can also do it using a handheld control unit (HCU) and an oscilloscope.
Depending on the digitiser type, sine-wave, step and broadband noise signal generators may be available. In this article, we will use a step input signal to determine sensor characteristics for a conventional-response velocity instrument. Step calibration is less useful for hybrid-response instruments.
-
In Scream!’s main window, right-click on the digitiser’s icon and select . Open the Calibration pane.
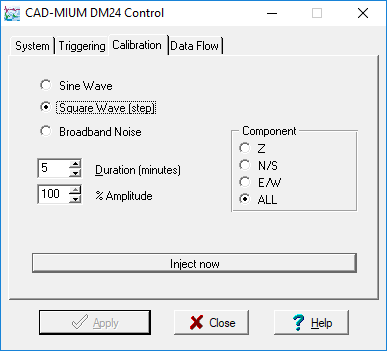
-
Select the calibration channel corresponding to the instrument, and choose . Select a suitable amplitude, make any other choices you require, and click Inject now.
A new data stream, ending Cn (where n = 0 – 7) or MB, should appear in Scream!’s main window containing the returned calibration signal.
-
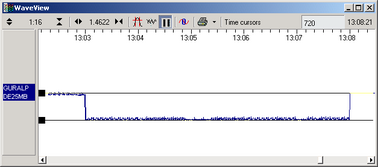
Open a WaveView window on the calibration signal and the returned streams by selecting them and double-clicking. The streams should display the calibration signal combined with the sensors’ own measurements. If you cannot see the calibration signal, zoom into the WaveView using the scaling icons at the top left of the window or the cursor keys.
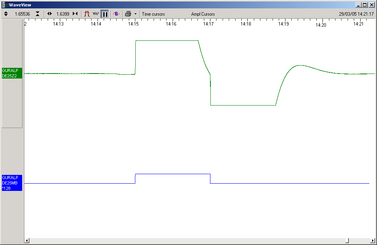
If the returning signal is saturated (i.e. the top and bottom of the waveform is flat, as in the picture above), retry using a calibration signal with lower amplitude, until the entire curve is visible in the WaveView window.
If you need to scale one, but not another, of the traces, right-click on the trace and select Scale…. You can then type in a suitable scale factor for that trace.
-
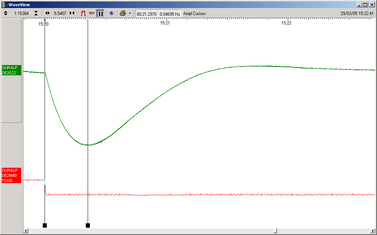
Click on Time Cursors in the top right hand corner of the window. A white square will appear inside the WaveView at the top left. This is, in fact, two superimposed cursors.
Drag one cursor across to the beginning of the returning signal, then drag the other across to be level with the first peak.
-
The Time Cursors button will now be displaying a value, which is the time period indicated in seconds.
-
The rise time to the first peak Tpk is related to the long-period corner frequency Tp by the equation:
Tpk = Tp / 5.656The example above was created using a 120 s sensor, so:
Tpk = 120 / 5.656 = 21.216 sThe measured value, 21.297 s, agrees with the theoretical result to within the margin of error of the experiment.
-
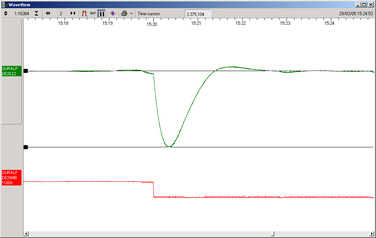
Click on Time Cursors once more, to remove them, and click on Ampl Cursors in the top right hand corner of the window.
Drag one cursor down to be level with the zero point of the returning signal trace, then drag the other down to be level with the first peak.
-
The Ampl Cursors button will now be displaying a value, which is the strength of the returning signal in counts. If you have used the Scale… option, you will need to take the scale factor into account to produce the correct number of counts.
-
Convert the number of counts into volts using the µV/Bit value given on the digitiser’s calibration sheet for the input sensitivity.
-
Measure the calibration input signal in the same way.
-
Convert this value into volts using the µV/Bit value given on the digitiser’s calibration sheet for the calibration channel.
-
Convert this voltage to a calibration acceleration using the equation:
a = V / RKwhere R is the value of the calibration resistor, and K is the feedback coil constant.
-
The calibration acceleration is related to sensor parameters by the equation:
V0 = 0.3244 H Vcal / Rcal ωn Kwhere V0 is the voltage of the first peak and H is the sensitivity of the component in V/ms-1. For a velocity system, where ζ = 0.707, ωn = 2πb, where b is the imaginary part of the complex conjugate pair of the long period corner. The equation can therefore be rewritten as:
V0 = aH / 19.369bwhere a is the calibration acceleration, above. H is given on the main calibration sheet. To find b, look for the single complex conjugate pole in the Poles and Zeros table.
For example, the Poles column for a 120 s CMG-3T might look like
POLES (HZ) -5.89 x 10-3 ± 5.89 x 10-3j -180 -180 -80In this case, the value of b is 5.89 × 10-3. If there are more than one complex conjugate pairs, the one with the smallest absolute value should be used. To compute the absolute value, add the squares of the real and imaginary parts and take the square root of the result. (It is not necessary to take the root when merely comparing.)
-
To obtain the velocity responsivity, rearrange the equation above to:
H = 19.369 bV0 / aThe measured sensitivity for a 1 Hz sinusoidal calibration signal is given on the sensor’s calibration sheet. Since the instrument has a flat velocity response over the pass-band, this method should give the same result.
