Chapter 4. Calibrating the Güralp 6T

4.1 The calibration pack

All Güralp sensors are fully calibrated before they leave the factory. Both absolute and relative calibration calculations are carried out. The results are given in the calibration pack supplied with each instrument:

Works Order : The Güralp factory order number including the instrument, used internally to file details of the sensor's manufacture.

Serial Number : The serial number of the instrument

Date : The date the instrument was tested at the factory.

Tested By : The name of the testing engineer.

There follows a table showing important calibration information for each component of the instrument, VERTICAL, NORTH/SOUTH, and EAST/WEST. Each row details:

Velocity Output (Differential) : The sensitivity of each component to velocity at 1 Hz, in Volts/ms-1. Because the 6T uses balanced differential outputs, the signal strength as measured between the +ve and –ve lines will be twice the true sensitivity of the instrument. To remind you of this, the sensitivities are given as 2 × (single-ended sensitivity) in each case.

Mass Position Output : The sensitivity of the mass position outputs to acceleration, in Volts/ms-2. These outputs are single-ended and referenced to signal ground.

Feedback Coil Constant : A constant describing the characteristics of the feedback system. You will need this constant, given in amperes/ms-2, if you want to perform your own calibration calculations (see below.)

Power Consumption : The average power consumption of the sensor during testing, given in terms of the current (in amperes) drawn from a 12 V supply.

Calibration Resistor : The value of the resistor in the calibration circuit. You will need this value if you want to perform your own calibration calculations (see below.)

4.2 Poles and zeroes

Most users of seismometers find it convenient to consider the sensor as a “black box”, which produces an output signal V from a measured input x. So long as the relationship between V and x is known, the details of the internal mechanics and electronics can be disregarded. This relationship, given in terms of the Laplace variable s, takes the form

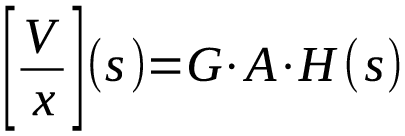
In this equation

• G is the output sensitivity (gain constant) of the instrument. This relates the actual output to the desired input over the flat portion of the frequency response.

• A is a constant which is evaluated so that A · H(s) is dimensionless and has a value of 1 over the flat portion of the frequency response. In practice, it is possible to design a system transfer function with a very wide-range flat frequency response.

  The normalising constant A is calculated at a normalising frequency value fm = 1 Hz, with s = j fm, where.

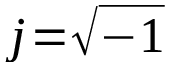• H(s) is the transfer function of the sensor, which can be expressed in factored form:

  

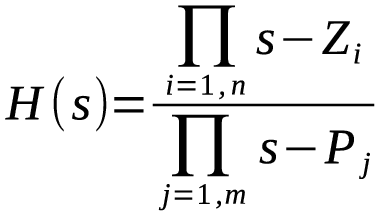
  In this equation Zn are the roots of the numerator polynomial, giving the zeros of the transfer function, and Pm are the roots of the denominator polynomial giving the poles of the transfer function.

In the calibration pack, G is the sensitivity given for each component on the first page, whilst the roots Zn and Pm, together with the normalising factor A, are given in the Poles and Zeros table. The poles and zeros given are measured directly at Güralp Systems' factory using a spectrum analyser. Transfer functions for the vertical and horizontal sensors may be provided separately.

4.3 Frequency response curves

The frequency response of each component of the 6T is described in the normalised amplitude and phase plots provided. The response is measured at low and high frequencies in two separate experiments. Each plot marks the low-frequency and high-frequency cut-off values (also known as –3 dB or half-power points).

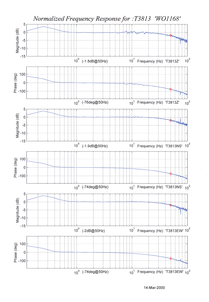
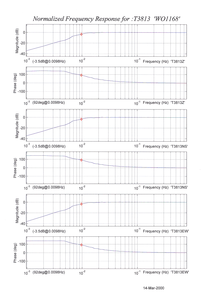
If you want to repeat the calibration to obtain more precise values at a frequency of interest, or to check that a sensor is still functioning correctly, you can inject calibration signals into the system using a Güralp digitizer or your own signal generator, and record the instrument's response.

4.4 Obtaining copies of the calibration pack

Our servers keep copies of all calibration data that we send out. In the event that the calibration information becomes separated from the instrument, you can obtain all the information using our free e-mail service. Simply e-mail caldoc@guralp.com with the serial number of the instrument(s) in the subject line, e.g.

The server will reply with the calibration documentation in Microsoft Word format.

4.5 Calibration methods

Velocity sensors such as the 6T are not sensitive to constant DC levels, either as a result of their design or because of an interposed high-pass filter. Instead, three common calibration techniques are used.

• Injecting a step current allows the system response to be determined in the time domain. The amplitude and phase response can then be calculated using a Fourier transform. Because the input signal has predominantly low-frequency components, this method generally gives poor results. However, it is simple enough to be performed daily.

• Injecting a sinusoidal current of known amplitude and frequency allows the system response to be determined at a spot frequency. However, before the calibration measurement can be made the system must be allowed to reach a steady state; for low frequencies, this may take a long time. In addition, several measurements must be made to determine the response over the full frequency spectrum.

• Injecting white noise into the calibration coil gives the response of the whole system, which can be measured using a spectrum analyser.

You can calibrate a 6T sensor using any of these methods, using the signal generator built in to all Güralp Systems' digitisers.

4.6 Noise calibration with Scream!

The most convenient way to calibrate a 6TD instrument is to use a Güralp DM24's pseudo-random broadband noise generator along with Scream!'s noise calibration extension. The extension is part of the standard distribution of Scream!, and contains all the algorithms needed to determine the complete sensor response in a single experiment.

Information on other calibration methods is available on the Güralp Systems Web site.

• In Scream!'s main window, right-click on the digitizer's icon and select Control.... Open the Calibration pane.

• Select the calibration channel corresponding to the instrument, and choose Broadband Noise. Select the component you wish to calibrate, together with a suitable duration and amplitude, and click Inject now. A new data stream ending Cn (n = 0 – 7) should appear in Scream!'s main window containing the returned calibration signal.

  

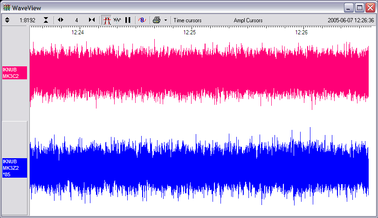
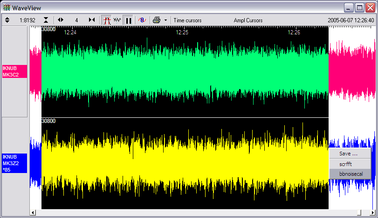
• Open a Waveview window on the calibration signal and the returned streams by selecting them and double-clicking. The streams should display the calibration signal combined with the sensors' own measurements. If you cannot see the calibration signal, zoom into the Waveview using the scaling icons at the top left of the window or the cursor keys.

  Drag the calibration stream Cn across the Waveview window, so that it is at the top.

• If the returning signal is saturated, retry using a calibration signal with lower amplitude, until the entire curve is visible in the Waveview window.

• If you need to scale one, but not another, of the traces, right-click on the trace and select Scale.... You can then type in a suitable scale factor for that trace.

• Pause the Waveview window by clicking on the icon.

• Hold down and drag across the window to select the calibration signal and the returning component(s). Release the mouse button, keeping held down. A menu will pop up. Choose Broadband Noise Calibration.

• The script will ask you to fill in sensor calibration parameters for each component you have selected.

  

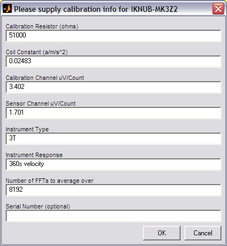
  Most data can be found on the calibration sheet for your sensor. Under Instrument response, you should fill in the sensor response code for your sensor, according to the table below. Instrument Type should be set to the model number of the sensor.

  If the file calvals.txt exists in the same directory as Scream!'s executable (scream.exe), Scream! will look there for suitable calibration values.

  See the Scream! manual for full details of this file. Alternatively, you can edit the sample calvals.txt file supplied with Scream!.

• Click OK. The script will return with a graph showing the response of the sensor in terms of amplitude and phase plots for each component (if appropriate.)

  The accuracy of the results depends on the amount of data you have selected, and its sample rate. To obtain good-quality results at low frequency, it will save computation time to use data collected at a lower sample rate; although the same information is present in higher-rate streams, they also include a large amount of high-frequency data which may not be relevant to your purposes.

  

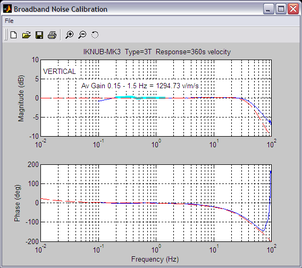
  The calibration script automatically performs appropriate averaging to reduce the effects of aliasing and cultural noise.

4.6.1 Sensor response codes

The standard response code for a 30 s to 100 Hz 6T is 30s100Hz with units V.

Sensor response codes for legacy responses are shown in the table below.

4.7 The coil constant

The feedback coil constant K is measured at the time of manufacture, and printed on the calibration sheet. Using this value will give good results at the time of installation.

If you wish to check it, the coil constant can be determined by tilting the instrument and measuring its response to gravity. To do this, you will need apparatus for measuring tilt angles accurately.

• Measure the acceleration due to gravity, g, at your location.

• Tilt the instrument slightly, and measure its attitude and the value of the mass position output for the component you wish to calibrate.

  To make it easier to measure mass positions, you should use the RESP command to place the instrument in 1 second response mode beforehand. To do this, open a Terminal window in Scream! and issue the commands

  OK-1

  1 RESP

  MASSES?

  0 RESP

  GO

• Repeat this measurement for several tilt angles.

• For the vertical sensor, the input acceleration is given by a = g sin φ, whilst for the horizontal sensor, it is a = g ( 1 – cos φ ).

  Calculate the input acceleration for each of the tilt angles used, and plot a graph of mass position output against input acceleration.

• The gradient of the line obtained gives the sensitivity of the coil (in V/ms-2, if g was measured in ms-2 and the mass position in V.)

• The coil constant K is equal to this sensitivity divided by the value of the displacement feedback resistor, given on the calibration sheet.